2 player dice game

So this is a dice game with some interesting game theory involved. I was a little surprised to find most solutions online seemed off to me so I solved it to find out.

Say we have a 30-sided die, and this game involves 2 players, A and B.

A will choose their number first, and then B will choose a different number.

Now we’re going to roll the die. Whoever chooses a number which is closer to the number that the die rolls will win the amount of money that the die rolled.

Would you like to be player A or player B?

Solutions posted online are the following:

The expected value for the roll is 15.5 so to maximize winning player A can immedietly get one of the closest positions to minimize distance.

16 is the better of the two 15 and 16

That can’t be true! Can it? Let’s find out!

To find out if it’s better to be player A or B, we need to find out what are the expected winnings for each player VS the other. There are three things we need to find out:

1. What is the optimal policy for B given A’s choice?
2. What is the optimal policy for A given B’s choice?

I think the first part is easier. For a given choice of A, what’s the best policy? When A chooses a value, they effectively split the problem into two dice games, and B’s choice is to pick which dice they want to be rewarded. If A picks 15, the expected value of winnings > 15 is naturally higher than those of < 15. Whatever B choses, A, automatically wins all the rolls on the opposite side, plus they share what’s in between them and B. Naturally, to limit A’s winnings, picking the roll immedietly adjacent to to their choice, minimizes their winnings for that choice. So the optimal policy for B is either A+1 or A-1, depending on which side has higher expected value.

Now that we’ve identified B’s optimal choice, next, is finding what’s the optimal choice for A. It’s a straight forward search problem, and the solution space is small so no issues there. Let’s set the problem up.

To calculate the expected winnings for both players, let’s create function calculate_expected_winnings:

# Function to calculate expected winnings for Player A and Player B
def calculate_expected_winnings(x):
    expected_winnings_A = []
    expected_winnings_B = []
    
    for n_A in range(1, n_sides + 1):
        winnings_A = 0
        winnings_B = 0
              
        if n_A <= x:
            # Compare the expected utility of choosing n_A - 1 vs n_A + 1 for B
            # This simplification assumes equal probability for all rolls
            # does not account for the exact expected utility calculation
            optimal_B_policy = n_A + 1
        elif n_A > x:
            optimal_B_policy = n_A - 1
        
        for roll in range(1, n_sides + 1):
            # Determine winner based on roll
            distance_A = abs(roll - n_A)
            distance_B = abs(roll - optimal_B_policy)
            
            if distance_A < distance_B:
                winnings_A += roll
            elif distance_B < distance_A:
                winnings_B += roll
            # In case of a tie, split the winnings (though ties are very unlikely in this setup)
            else:
                winnings_A += roll / 2
                winnings_B += roll / 2
        
        # Calculate expected winnings
        expected_winnings_A.append(winnings_A / n_sides)
        expected_winnings_B.append(winnings_B / n_sides)
    
    return expected_winnings_A, expected_winnings_B

Now we search and generate the plot:

# Search for the optimal choice
total_expected_winnings_by_x = [calculate_total_expected_winnings_for_B(x) for x in range(1, n_sides + 1)]

# Find the x with the highest total expected winnings for Player B
optimal_x = total_expected_winnings_by_x.index(max(total_expected_winnings_by_x)) + 1

# Calculate the expected winnings for Player A and Player B at the optimal x
expected_winnings_A, expected_winnings_B = calculate_expected_winnings(optimal_x)

Plotting the results:

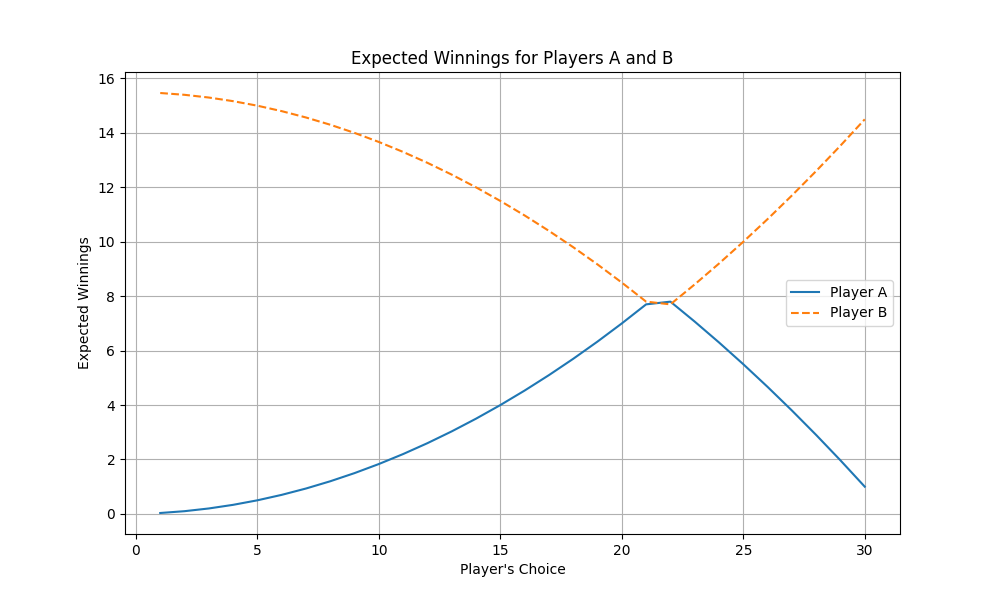
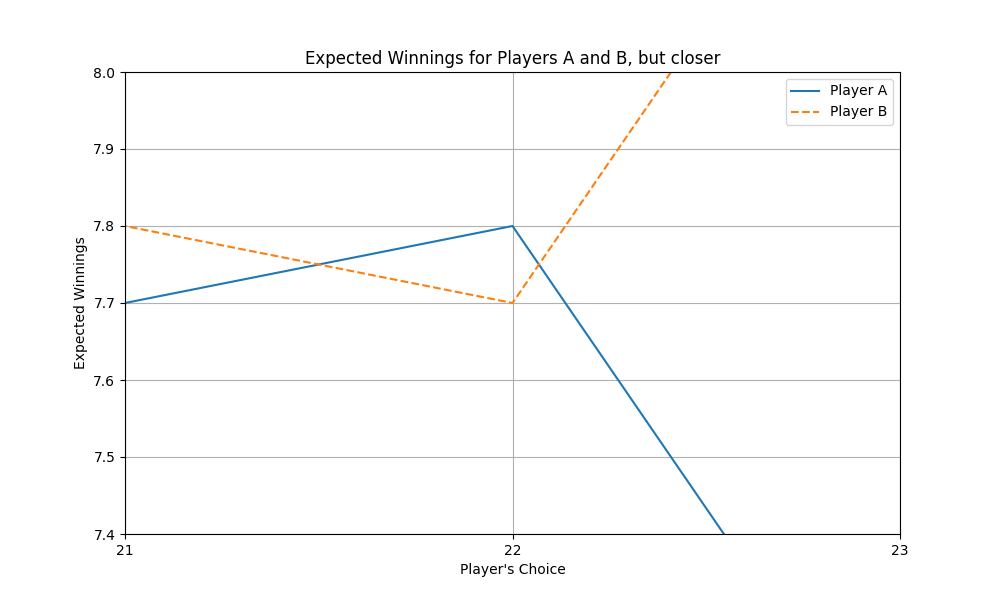
Ok so knowing what we know, in absolute terms, player A can have the highest expected return when choosing 21. But I wouldn’t want to be player A for that small of an edge, with that huge downside (significantly less winnings for the rest of choice). I would take B as in the worst case scenario, I am better positioned to win “almost” as much as A, if they play perfectly. Otherwise, I have much higher upside.